We recently submitted a proposal to optimize street sweeping and garbage collection routes for the city of Glendale, California. This blog post covers some things we learned about setting up the problem using open source data, tools, and libraries.
From assignment to edge covering
This project is different from the usual applications of the OR-Tools routing solver. A typical vehicle routing problem requires guiding a vehicle optimally from destination to destination. In contrast, street sweeping is an edge covering problem. The edge of the street is literally being covered by the street sweeper’s brooms. Instead of visiting a countable set of addresses, the goal is to visit all the streets using an efficient path.
Edge covering is a classic problem, tracing its origins all the way back to the Königsberg bridges problem famously solved by Leonhard Euler in 1736. In 1960, the Chinese mathematician Kwan Mei-Ko studied and solved the problem of a postman needing to traverse the minimum number of links in an undirected network in order to deliver mail. This “Chinese Postman Problem” can be solved in polynomial time, but variations of this problem have been shown to be NP-Complete or NP-Hard. In a mixed network, in which some links are bi-directional and others are one-way, or in the rural postman variant in which some links do not need to be covered, the problem is NP-Complete. Practically speaking, this means that for any real-world instance of planning street sweeping or garbage collecting routes, the polynomial time algorithm is not applicable.
Edge covering problems require the underlying logical travel network to be modified. This is because instead of visiting nodes that are connected by travel along the roads, in an edge covering problem the goal is to visit the edges themselves. The usual transportation network needs to be inverted, with each street curb turned into a node that must be visited, connected by links that represent legal traffic movements from curb to curb. The links no longer model physical streets. Instead the links model allowed movements.
The process of converting a traffic network graph so that the links become nodes is known as building a “Line Graph” of the original graph. The wikipedia page on the topic is reasonably good at describing the process, and I make my own attempt below. Once the line graph is constructed, then the problem can be solved using the usual traffic routing approach. If every node has to be visited, then the shortest route will obviously contain as many zero-cost transitions from street-edge to street-edge as possible. If, when deciding on the “next edge” to visit, it turns out that all of the adjacent edges have already been visited, then the optimal route will be the one with the fewest repeated edges. By minimizing the overall path length, the solver should be able to find a good street sweeping route for all of the vehicles that obeys all of the constraints.
So that’s the plan: get some street network data, turn it into a line graph, and use OR Tools. For the source data, we knew we wanted to use OpenStreetMap. The data is free to use, and is pretty good for most cities in the US. While using it in practice will require spending some time verifying the network, OSM is perfect for proposals and exploratory work. The work was actually in getting from the raw OSM input data to a point where we could use our OR-Tools solver tricks. The rest of this blog post describes our lessons learned in massaging the data from OSM file into the required line graph. The next two sections talk about some libraries we tried to use to extract and use OSM data. These are followed by a section on fixing up the OSM links. Next we talk about how to create a line graph, including how to handle our need to drive on both edges of a street. Then comes a short section describing the final line graph itself, and conclude with a few paragraphs on the first version of the solver we developed.
OSRM, Valhalla, Osmium, and NetworkX
Our usual choice for the routing server backing OR Tools is the Open Source Routing Machine, or OSRM. This project can parse and load OpenStreetMap data into a custom C++ routing library designed to quickly return point to point distances and directions. We’ve used the project many times, and have a reasonable cookie cutter Docker image on GitHub. This image is designed such that with a few tweaks, we can download and prop up an OSRM routing server for any State or metropolitan area.
Unfortunately, we couldn’t use OSRM directly for this problem, as it transforms the OSM networks into an opaque internal network representation. There is no API to generate and use a line graph transform. The more we poked at the problem the more we realized that there is a downside to a fast, customized C++ library—the library is not supposed to be a general purpose graph algorithm library. You can’t even easily grab the underlying OSM graph from within C++ to convert it yourself, as explained in this github issue. So I went fishing for a new library to use.
Next up was Valhalla. Both OSRM and Valhalla are developed predominately by MapBox programmers, and so they are both active and well maintained. Valhalla has some interesting ideas around generating a tiled view of the graph network, similar to how quadtiles work for mapping the world in most “slippymap” implementations on the web. More detail requires smaller tiles (a higher zoom level), but long straight portions of a route can be encoded more efficiently using larger tiles. However, once again, there was no way to reach in and change the underlying OSM network into its line graph dual.
Given that the fast but customized C/C++ libraries wouldn’t work, I
decided to go back to just extracting OSM data directly and building
my own network. We’ve done that
before using the Osmosis
library. Since Osmosis is currently
unmaintained
I thought I’d look into using
Osmium to parse the OSM data and
dump out road segment data as a simple CSV file. Then, using that CSV
file as input, I could create the line graph by using the python
library NetworkX. The NetworkX stuff
was fairly easy to figure out, and the whole process worked okay for a
test case. I wrote up a short test program—shown to the right—to make
sure the line graph call worked as expected. This worked fine on a
small scratch network. Although I wasn’t yet handling roads, curbs,
one-way and two-way links properly, NetworkX’s line_graph call
clearly handles directional graphs, and Osmium seemed to be pretty
fast at reading in OSM data.
So I dug in deeper, expanding the read-in step to pull in more information from OSM. Instead of pre-running osmium and generating a CSV file, my idea was to embed the Osmium processing inside the Python call, to both extract and add additional data (like road lengths) on the fly. Osmium is interesting, can do the job, has very useful Python bindings, but I ran into an issue. What I wanted to do was to extract the length of each segment, not just path’s latitudes and longitudes. This is possible if you transform the geometry into an appropriate projection that will give meters (or feet, if you are so inclined).
import os
import sys
import csv
import networkx as nx
G = nx.Graph()
# testgraph.csv generated by Osmium command line program previously
with open('testgraph.csv') as csvfile:
graphreader = csv.reader(csvfile)
for row_number, row in enumerate(graphreader):
try:
start_node = row[0]
end_node = row[1]
length = float(row[2])
id_ = row[3]
G.add_edge(start_node, end_node, weight=length, id=id_, label=id_)
except ValueError:
print("Skipping input row %d, %s" % (row_number+1,row))
print("input graph")
print(sorted(map(sorted, G.edges())))
L = nx.line_graph(G)
print("converted to line graph")
print(sorted(map(sorted, L.edges())))
However, it turns out that the binary
versions of pyproj and osmium available on pypy were using
different versions of the proj library. This led to some strange
errors and a github
issue. A simple
Python program that demonstrates the crash is shown to the right. One
of the maintainers of pyosmium pointed out the need to do source
installs for both libraries. I did so in a Dockerfile, and all is
well, but in the meantime I had soured on using Osmium and NetworkX
and instead had moved on to trying PGRouting.
(There just so many bugs I can handle before I choose a path with less resistance.)
import pyproj
import osmium
crs = pyproj.CRS.from_epsg(4326)
print(crs)
PostgreSQL, PostGIS, and pgRouting
And so back to my tried and true PostgreSQL, PostGIS, and pgRouting.
I’ve been using pgRouting for a
while on the margins of various projects. It is pretty good, has been
maintained for years, and lives in the PostgreSQL/PostGIS
ecosystem—one I am very familiar with. This means that once data is
“loaded” for use with pgRouting, it is also available using normal
SQL queries, and using spatially enhanced queries made possible by
PostGIS. The only downside that I could find was that the standard
OSM reader binary,
osm2pgrouting
does not process the newer protobuffer style OSM files. All that
means is I had to run an extra step to convert the pbf files to
osm format. I took advantage of that need and at the same time
chopped down the full state of California OSM file to just the city I
was interested in using the polygon outlining the city. From the
osmium documentation, this is as simple as:
osmium extract -p glendale-boundary.osm \
-o glendale-latest.osm \
socal-latest.osm.pbf
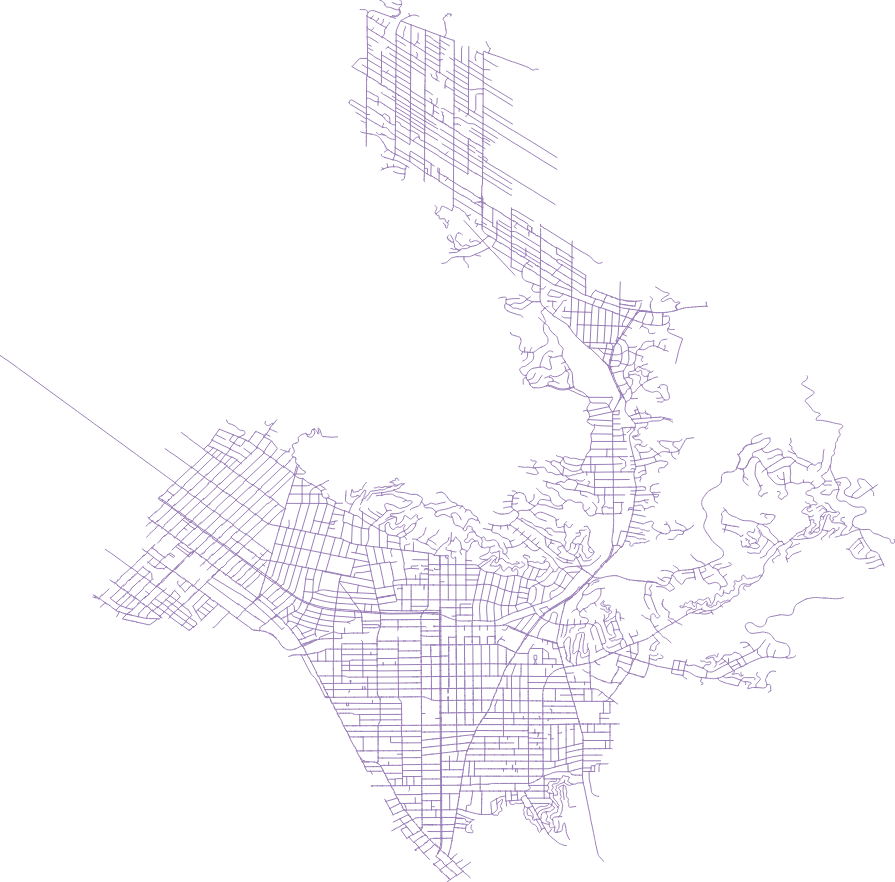
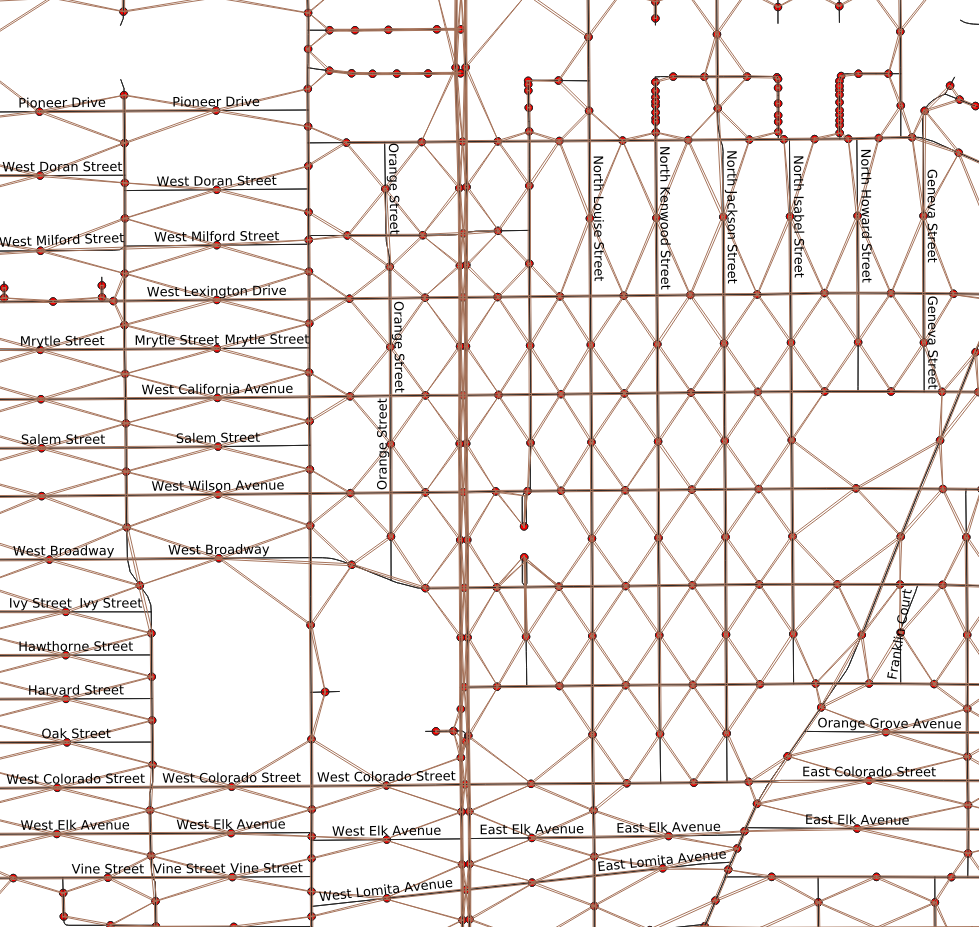
This reduced the Southern California OSM file to just those ways that are contained in or overlap the city of Glendale. After trimming some features I’m uninterested in (all polygons, freeways and service roads, etc), the resulting network table has 7,674 entries. Some of these links are not part of the city, and others form isolated leaf nodes or links that were ignored. The street map, as rendered by QGIS, is shown in the map to the right. There are some extra segments, as the cutting-out process includes “ways”, not just the individual segments. So the really long way that extends all by itself off to the northwest will be truncated in a real project.
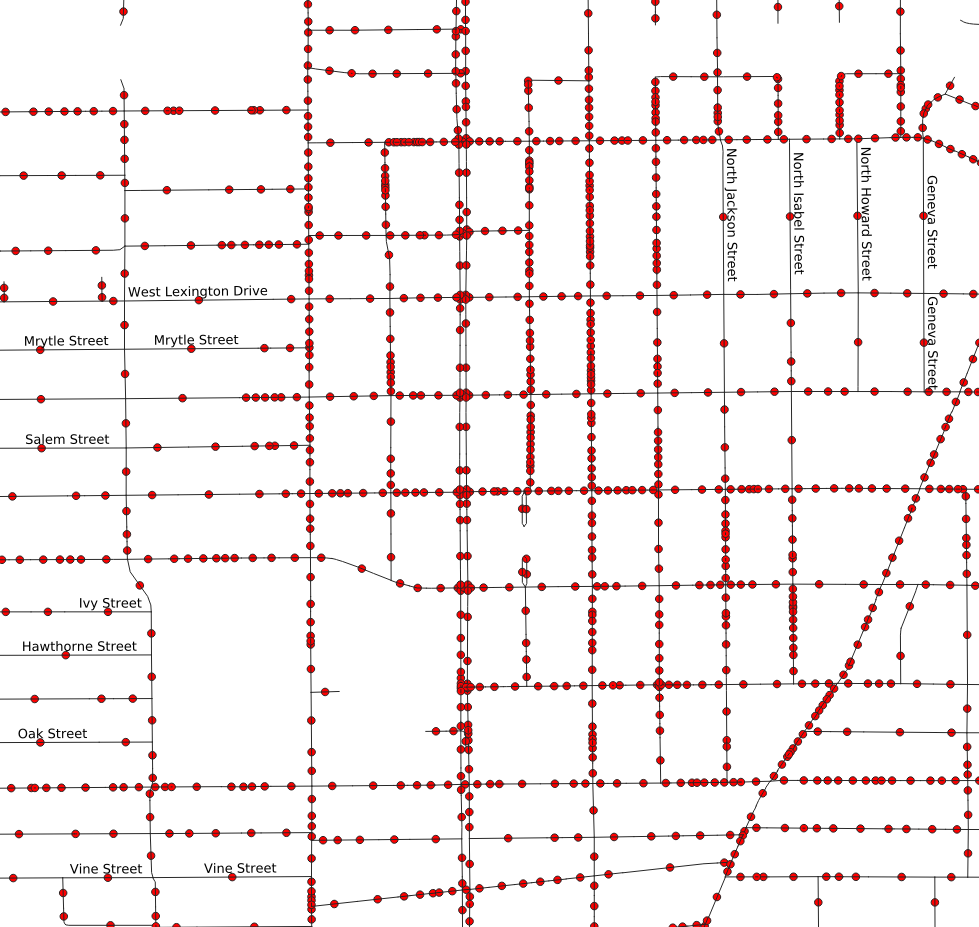
Too many segments per street
There is a hidden problem with the that street map. While it looks like a nice neat series of connected road segments, it is actually a huge messy pile of way too many segments. OSM data is designed for many purposes, not just for routing. The source data isn’t necessarily as clean as it can be for routing or edge covering problems. The problem with the City of Glendale data is that many of the roadway segments between intersections are broken up into multiple sub-segments. The figure to the right illustrates this by placing a dot in the middle of each link. Instead of one dot between each intersection, for most streets there are many of these dots. When the graph is transformed into a line graph, each of these sub-segments will become a required node visit—4, 6, or even 10 nodes to consider visiting, instead of just one. This greatly expands the size of the problem the solver will need to solve.
What is needed is to simplify the road segments between
intersections, such that there is just one segment, not multiple ones.
Doing so is a long and complicated job in PostgreSQL, made possible
through the use of WITH RECURSIVE..., but it is still about 300
lines of SQL code and well beyond the scope of this post.
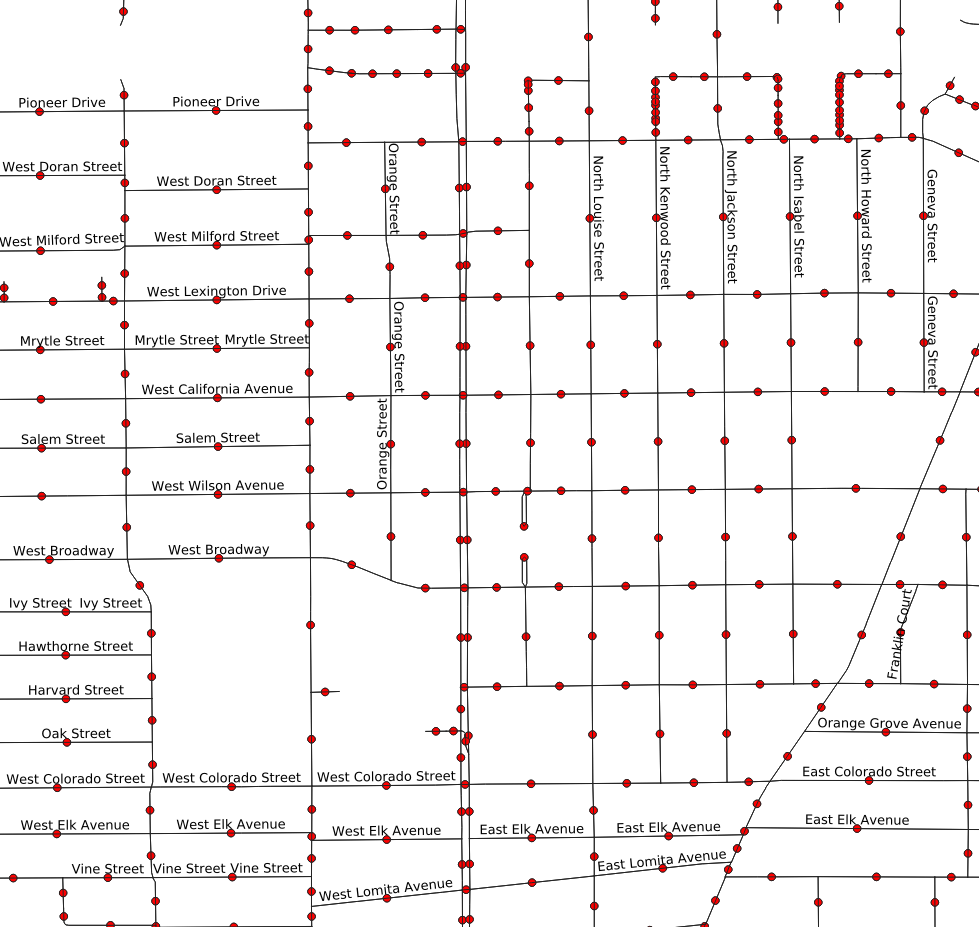
The end result looks okay, and is demonstrated in the figure to the right. The multiple midpoint markers have mostly gone away, replaced with just one dot showing that those multiple segments have been successfully merged into a single segment. The labels in the map are proof of this—QGIS can fit the labels in more easily when there is only one segment per city block, rather than the many there were originally. Note that if you form the line graph of the original, un-cleaned OSM-based graph, the resulting line graph table has over 192,000 edges. After merging together the multiple segments, the resulting line graph table has only 28,000 edges, which is about an order of magnitude improvement. This translates directly into a much faster running time for the solver, with the initial solution coming in at about 3 to 5 minutes rather than 20 to 30 minutes.
Finally, note that even with 300+ lines of SQL, there are still some issues with the de-segmentization code. Along the top edge of the second “fixed” figure, there are several streets with multiple segments each. This crops up here and there throughout the graph, typically with one-way roads. This indicates there is room for improvement in the SQL, although it is good enough for the first iteration, exploratory proposal phase.
The next problem that needs to be addressed is that the data pulled
and truncated from OpenStreetMap for the City of Glendale is not
strongly connected. That is, inside of the graph, there are nodes
that cannot reach all the other nodes in the graph. Of course this
makes no sense in real life, as it is purely an artifact of cutting
out the city of Glendale from the surrounding cities. In the real
world, the street sweeper or garbage truck can just move into the next
city over to maneuver so as to reach any isolated streets. In the final
project this will be corrected by adding links, but for the proposal
it was easier just to drop the unconnected streets. The pgRouting
library has a handy function called pgr_strongComponents that lets
us examine this:
with
components as (
select component,node from pgr_strongComponents(
'SELECT gid as id, source as source, target as target, cost, reverse_cost FROM ways' )
)
select component,count(*) from components group by component order by count(*) desc;
component | count
-----------+-------
1 | 6477
2692 | 2
1938 | 2
1932 | 2
...
5739 | 1
4249 | 1
(22 rows)
As can be seen from the truncated output above, the vast majority of nodes in the original graph belong to a single component, and the remaining 21 other components have either 2 or just 1 node in them. In order to solve any transportation problem, the isolated components must either be connected or dropped. Using a short bit of SQL, the 21 isolated components were dropped, leaving just the single main component.
Creating a line graph for the street network
With the data extracted from OSM files and loaded into the database, the next step is to create the line graph of the original graph. A standard routing network models intersections as nodes, and the roads between intersections as edges. This model of the road network is useful for providing directions or discovering a shortest path. However, this model is not useful for an edge covering problem. In the standard network, there is no way to require the visit of a particular link, as links only exist to connect intersections. In order to solve edge covering problems, the logical model of the roadway network needs to have a node for each road, and then edges between those “road-nodes” whenever it is legal to transition from one road to another. This modified graph is called the “Line Graph” of the original graph. Links represent legal movements. For example, if a vehicle can keep moving straight from one block to the next block, then there will be a link between the two nodes. On the other hand, if the vehicle comes across a one-way street and wants to turn onto it, it can only turn in one direction. The turning movement going the wrong way down the one-way street will not be included in the line graph as a link. All this is a bit abstract so the following paragraphs present more detail, with pictures.
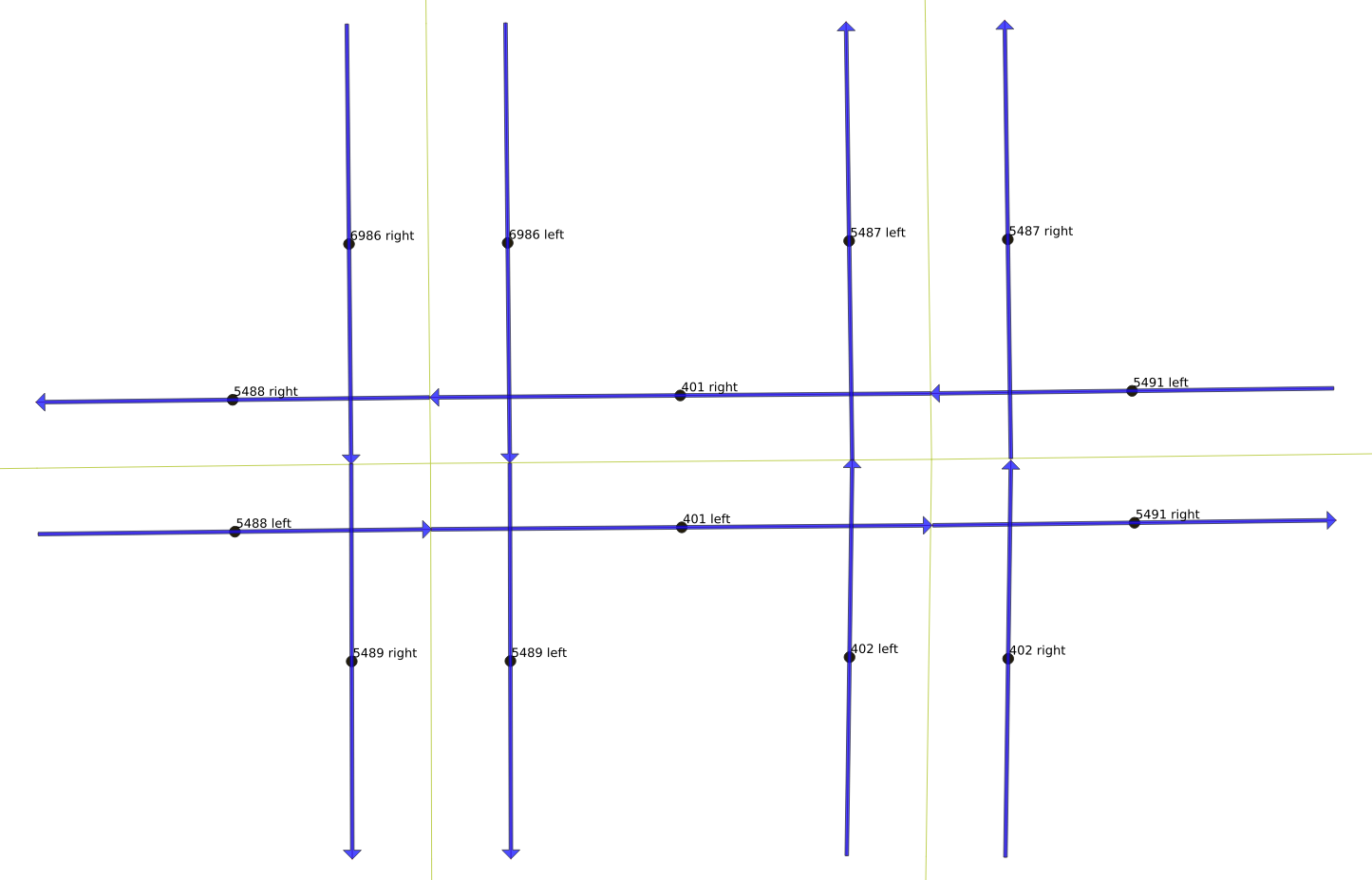
We took two steps to convert the usual roadway graph into a line graph. First, each roadway has two curbs. On a two-way roadway, each curb is on the right hand side of the normal direction of movement. For a one-way road, however, there is a right hand side curb, and a left hand side curb. So the first step was to create a curb-side graph, in which the one way links are split into two curb links, move moving from the same source to the same target, one for the left curb and the other link for the right curb. The two way links were also split into two curb links, but one moving from source to target to represent the right hand side curb, and the other link from target to source to represent the right hand side curb of the opposite direction of movement.
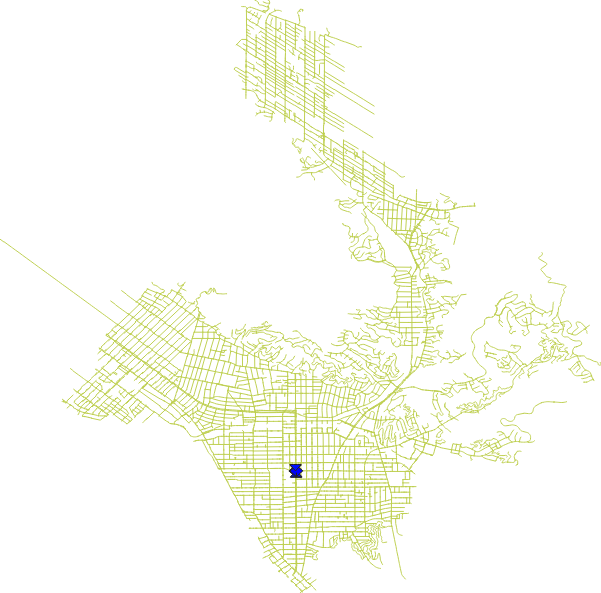
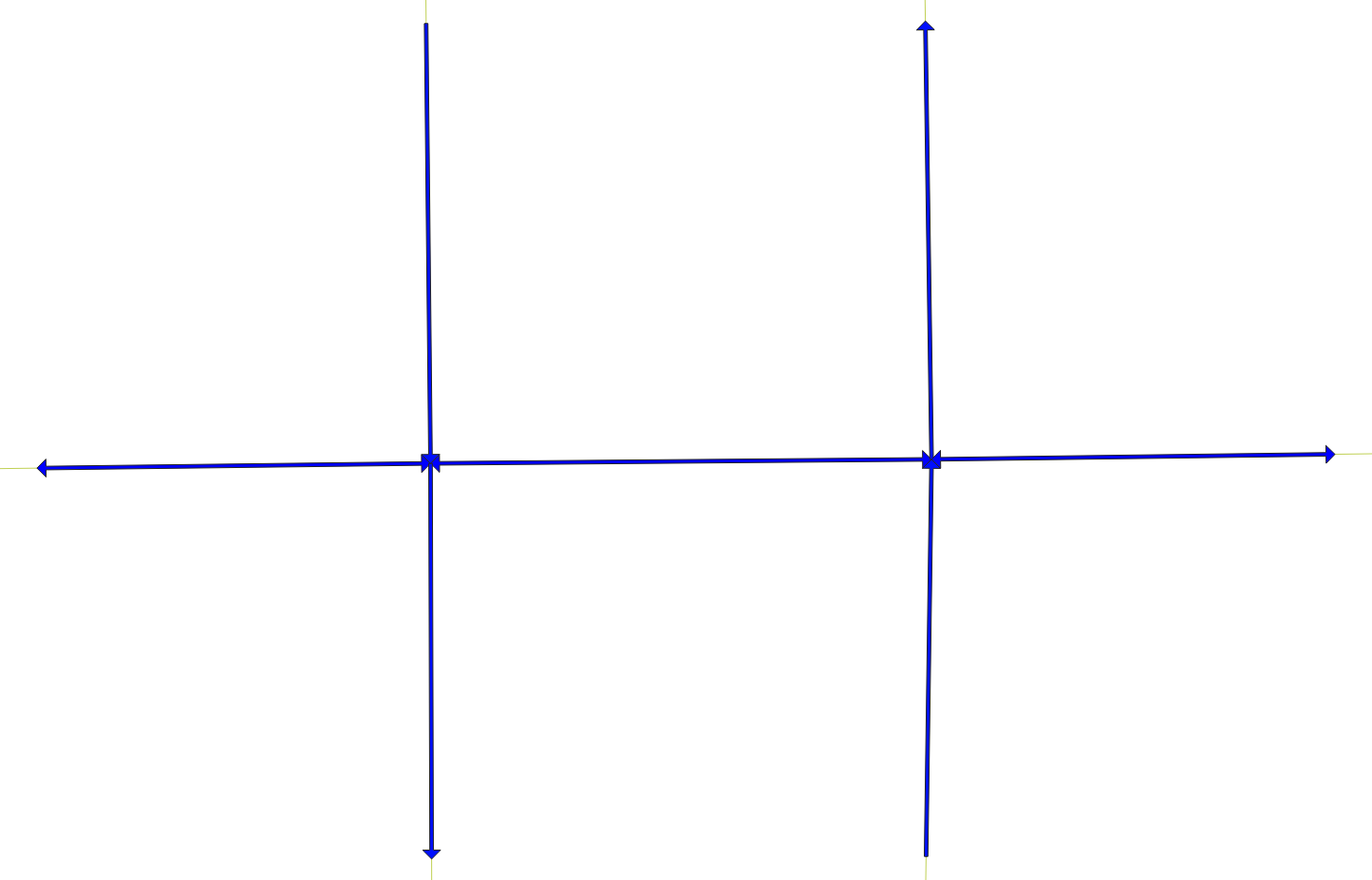
This is illustrated in the figures to the right. (These pictures are a bit small on this page, but you can click on them to get bigger versions.) We snipped just a few links out of all of Glendale, shown by the blue dot in the figure above right. The figure below that is zoomed in to just the few links, with the directionality of each link shown by the blue arrows. The horizontal links are two-way, while the vertical links are one-way. The left hand vertical links are moving north to south (top to bottom), while the right hand vertical links are moving south to north (bottom to top).
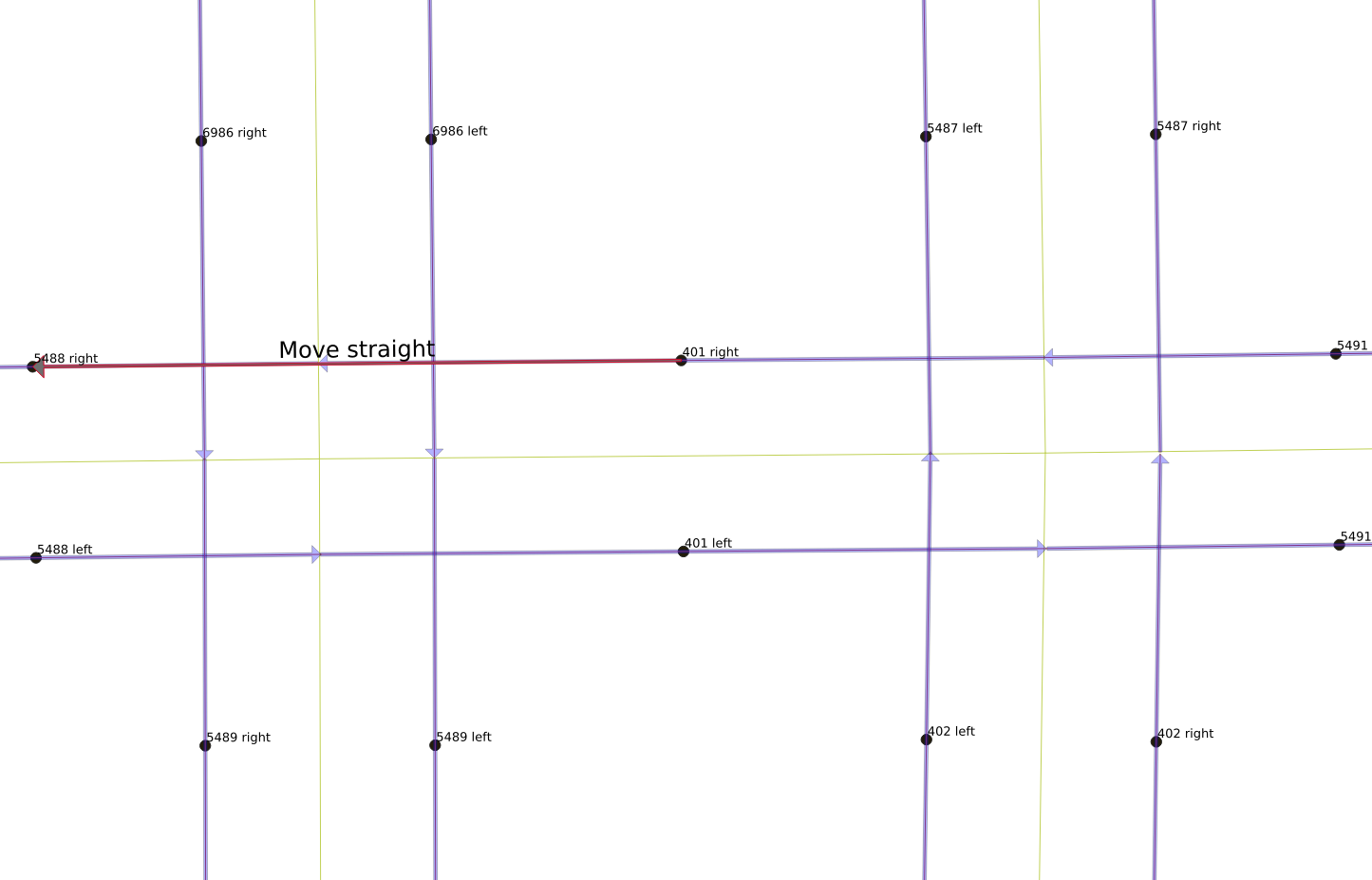
The next figure accentuates the directionality of each curb-side link by separating left and right sides of the roadway. The two-way horizontal roadway has been split into left to right links, and right to left links. The one-way roads, in contrast, have been split into two sets of links moving in the same direction. One interesting quirk of working with a generic graph is that the right most roadway segment is constructed left to right, while the sense of the line segment for the rest of the road is right to left. This means that the node labels are slightly different. Link 5491 is defined such that it starts at the intersection and ends at the edge of the figure. This means that following the sense of that movement, the north curb is defined as the left hand side, while the south curb is defined as the right. However, following the usual North American practice, the south side of the roadway moves left to right, while the north side moves right to left. The labels for links 401 and 5488 are different, because the roadway lines start at the intersection with link 5491, and move to the left, with 401 ending at the intersection with link 5488, and 5488 ending at the left hand side of the figure. Following this sense of movement as the primary direction of the link, the north side of these links is labeled as “right”, while the south side is labeled as “left”. In truth, the labeling is irrelevant in the end, but it is important to realize that there is no guaranteed sense of rendering direction for the line segments in OpenStreetMap data.
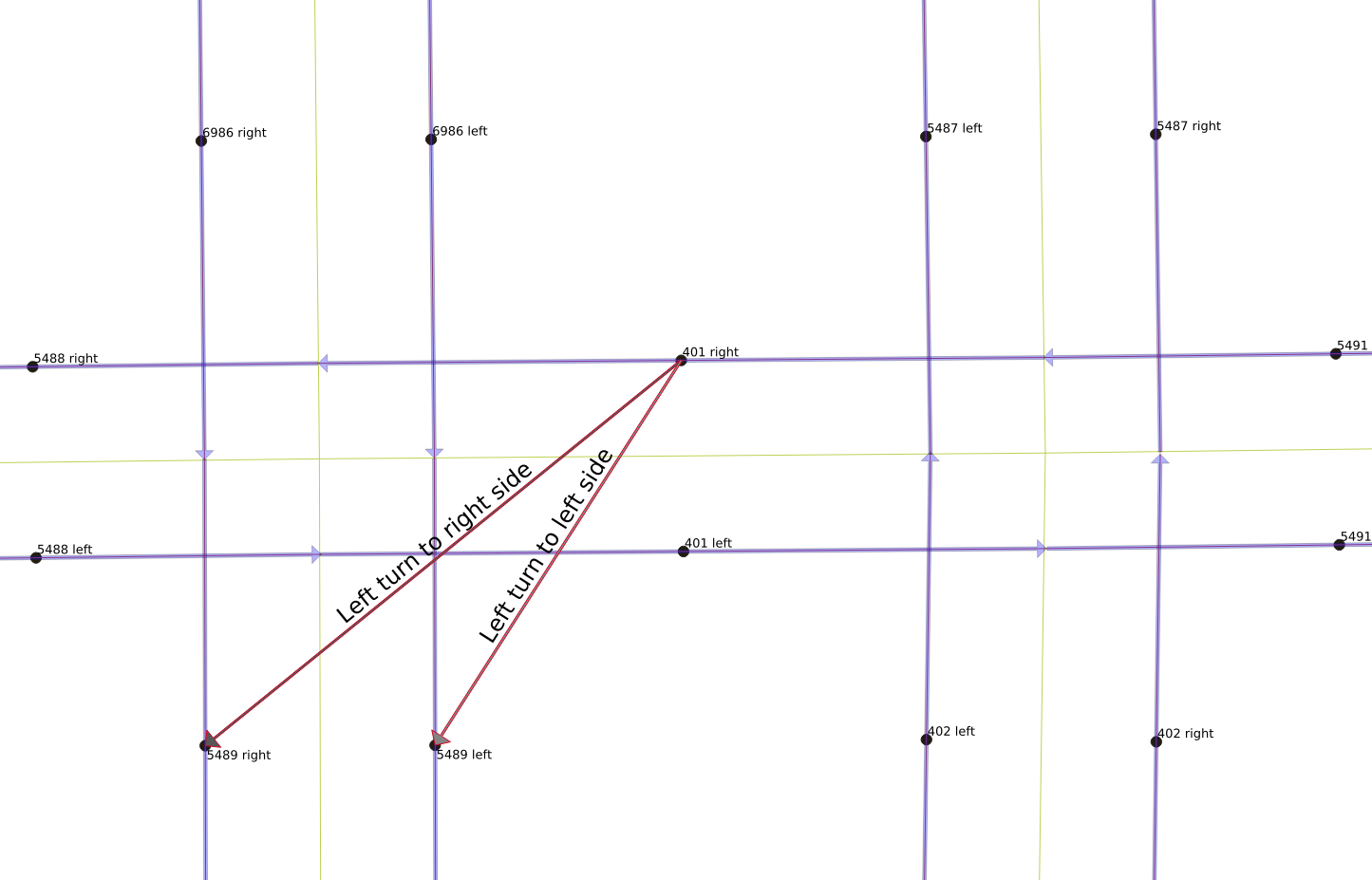
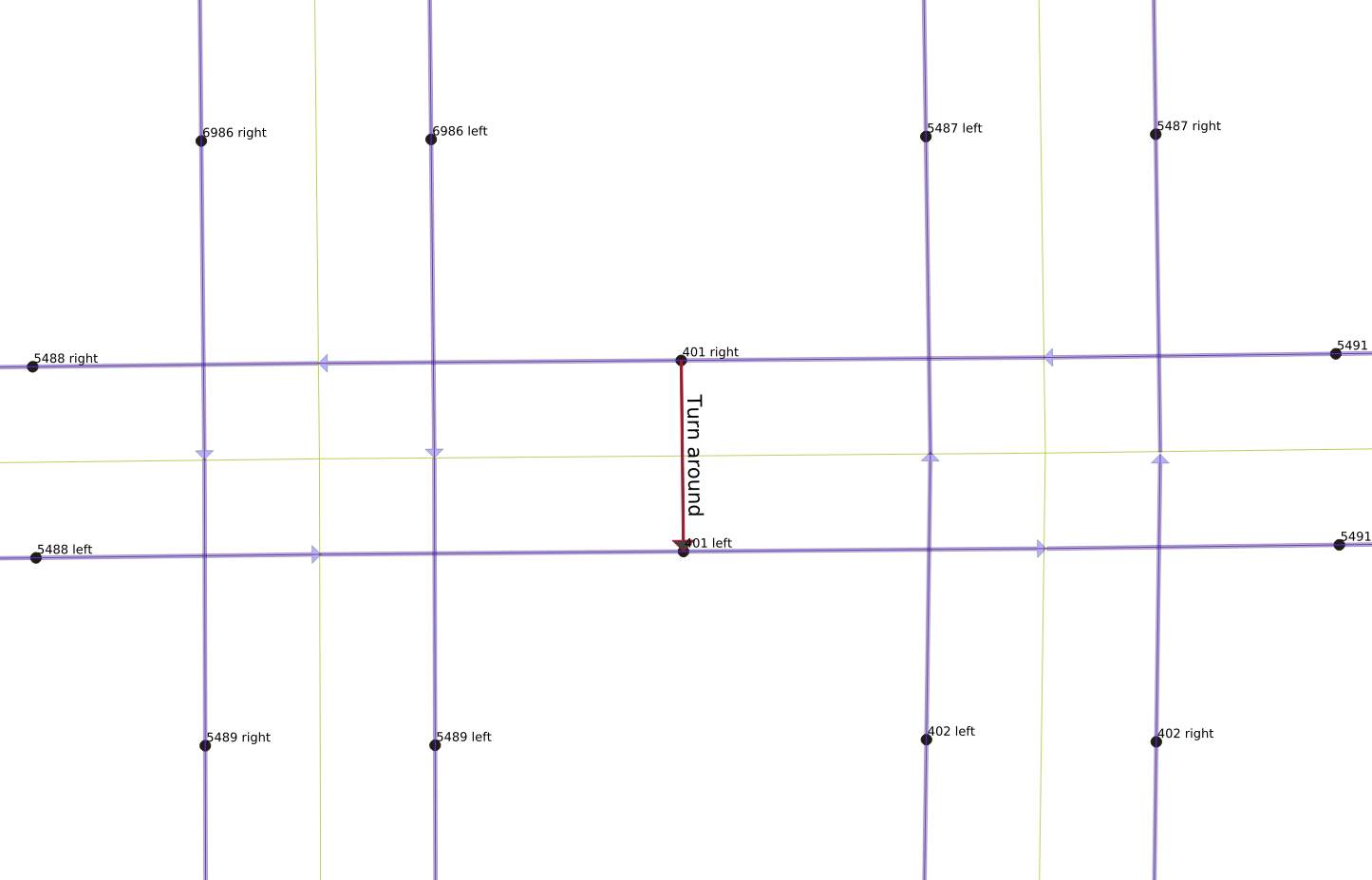
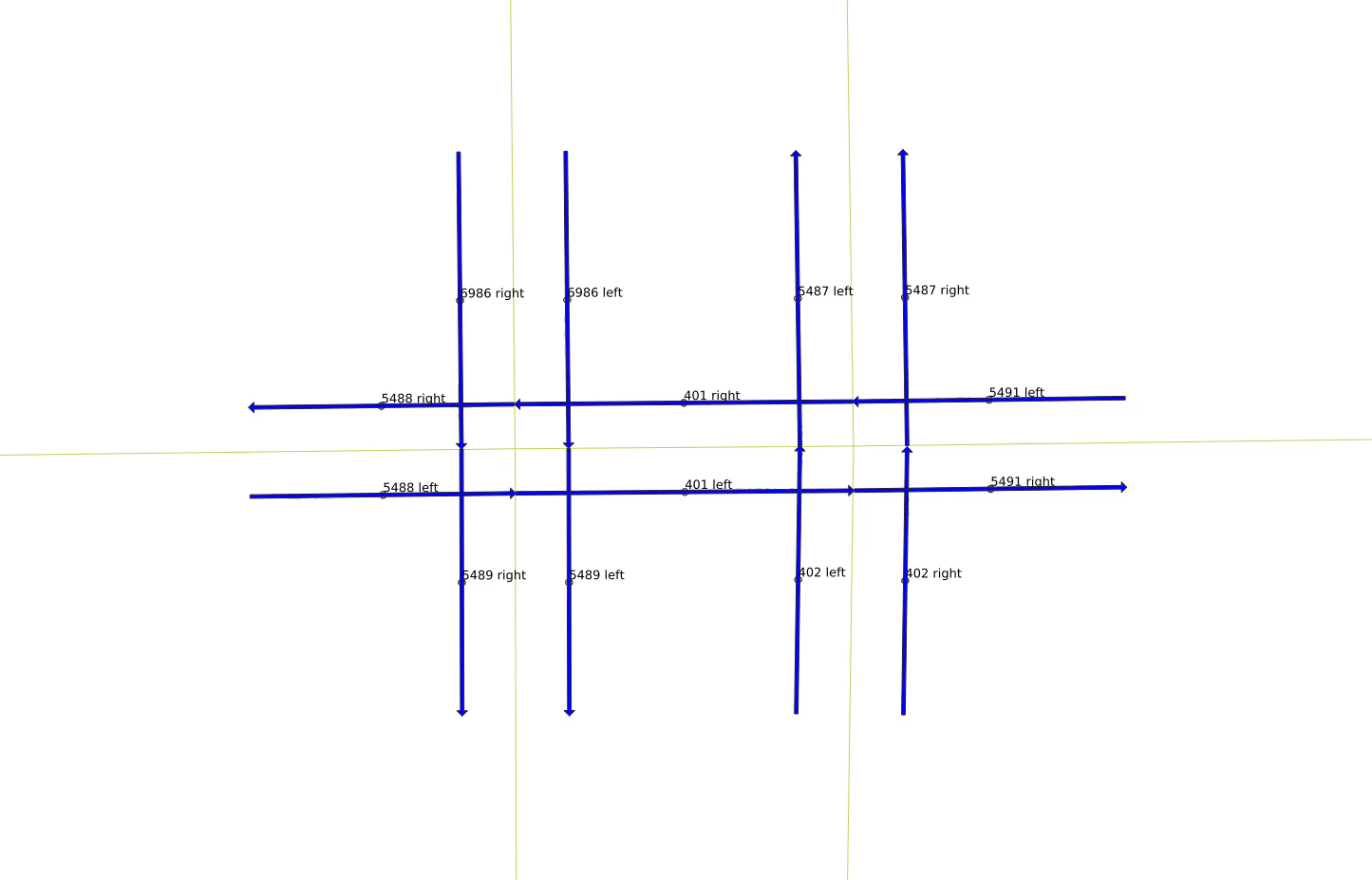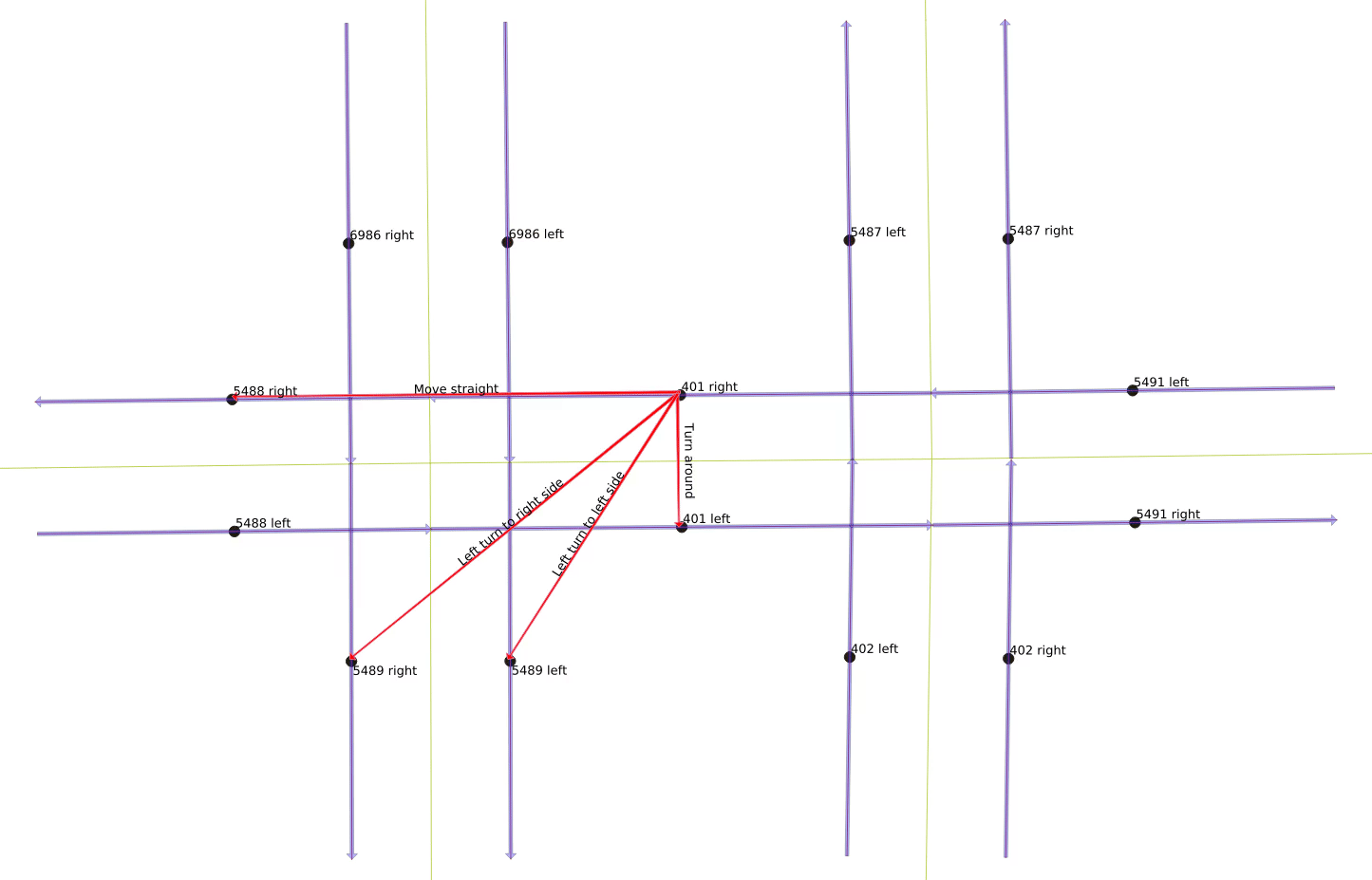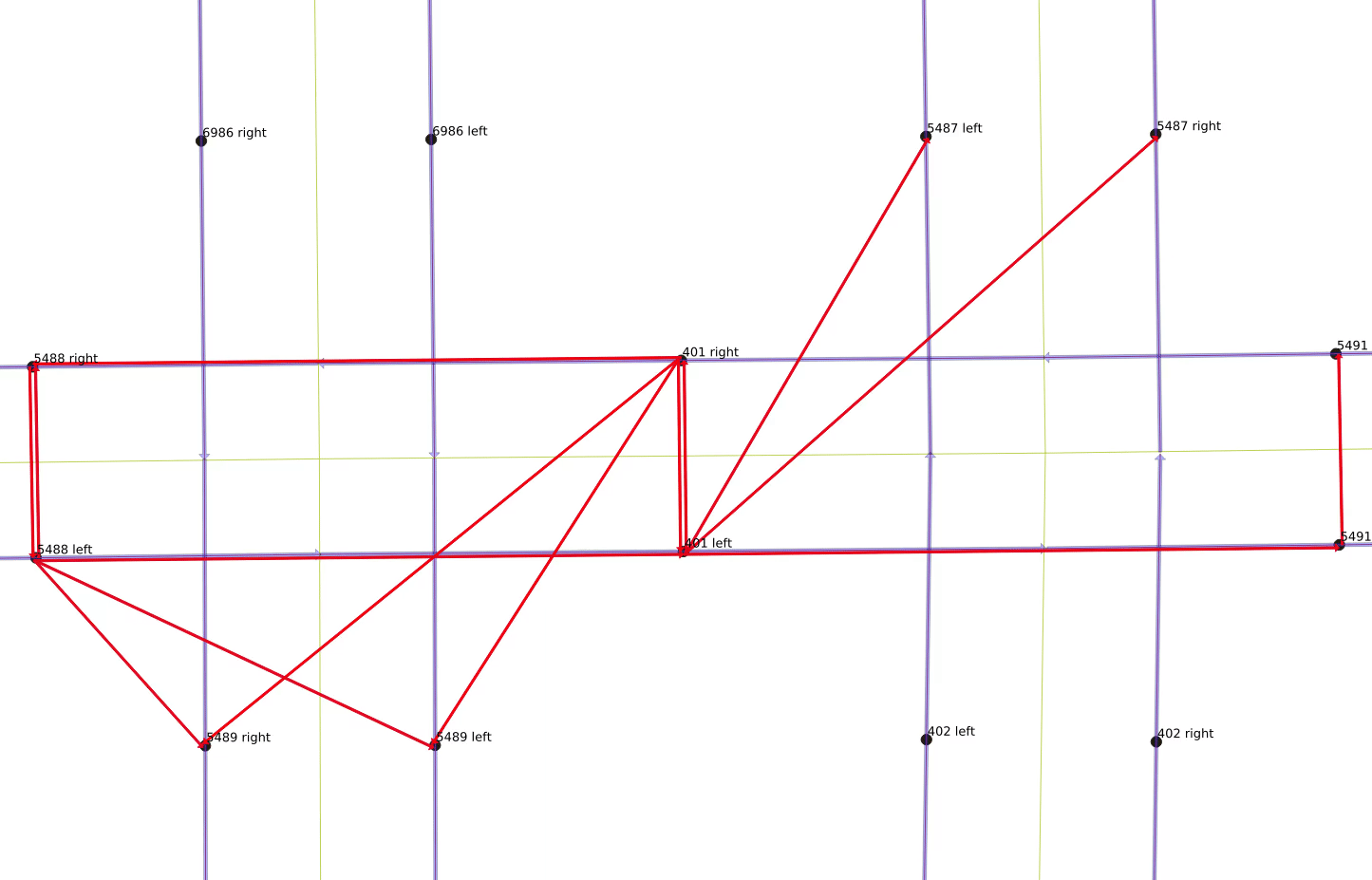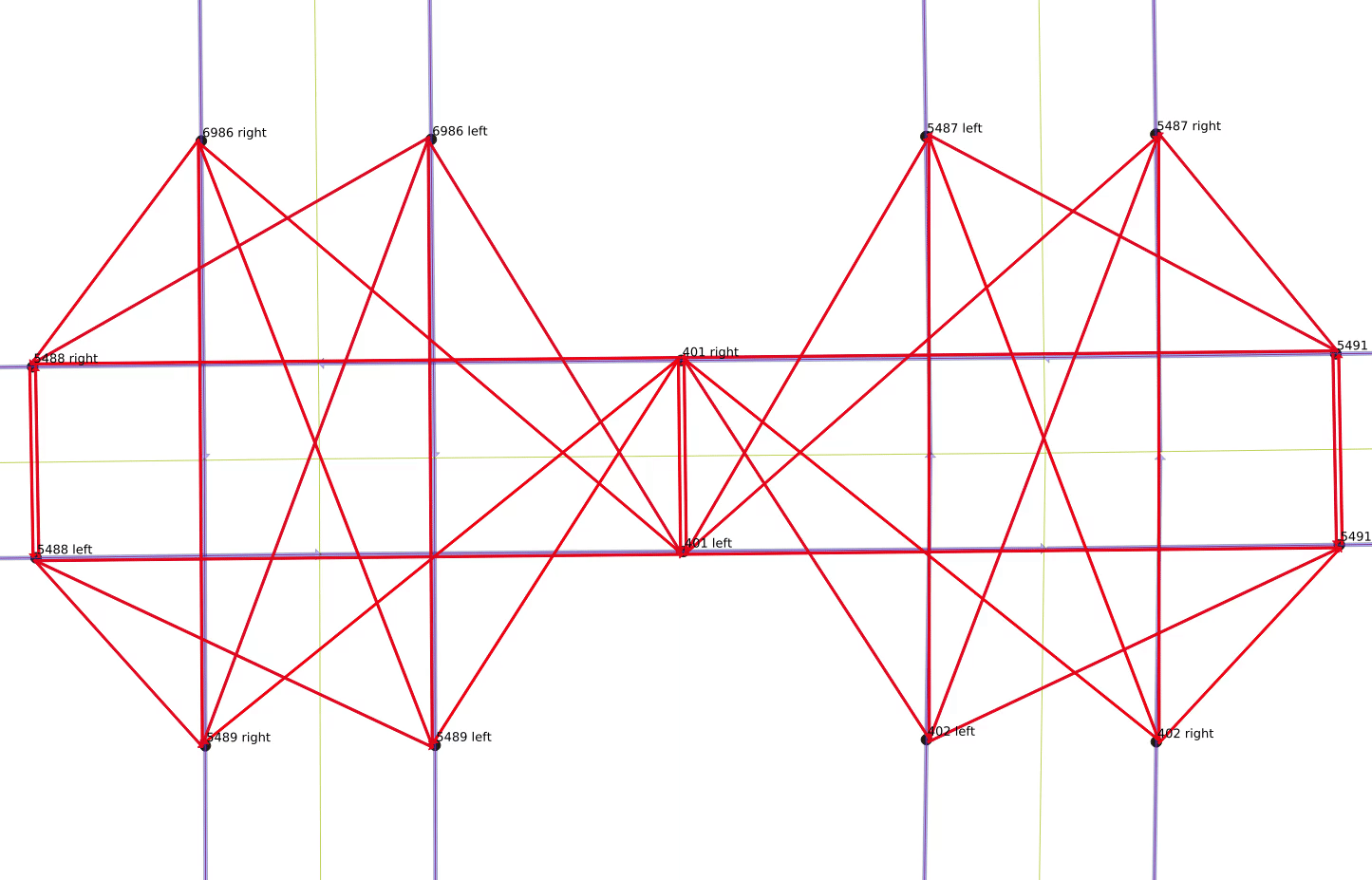
There are legal and illegal movements from each link. The next three figures show the legal movements off of link “401 right”. A vehicle on that link can either keep moving straight, as shown to the right, or it can turn left onto either side of the one-way north-south link 5489, or it can make a U-turn and move back the way it came on link “401 left”, as shown in the below-right figure. However, it is not legal for it to make a right turn, however, and it also cannot move backwards to any of the other links.
A small animation of all of the legal movements that make up the total line graph is shown below.
Generating the final line graph
The stored function for generating a line graph from a graph in pgRouting does all the real work. The function call is useful even on the original mixed graph with two-way and one-way links, but it has a few quirks that are difficult to interpret. Specifically, if presented with a two-way link, it will label the reverse movement on that link with a negative. So referring to the figure above, link “5491 left” would be kept as 5491, but “5491 right” would be labeled -5491. Similarly, “401 right” is 401, and “401 left” becomes -401, because link 401 is specified in the opposite direction from link 5491. That means link 5491 connects in a straight line to link -401, and since it is a two-way link, the line graph has a positive “reverse cost” entry meaning that link 401 can move to link -5488.
In theory this seems like a reasonable approach, but in practice it is a miserable headache, and requires multiple case statements to handle properly. It is much cleaner to just stick with the uni-directional curb-side links. This “curbside graph”-based line graph works better because the resulting nodes (representing the road sections) all have unique ids and there are no negative ids (as there are no non-negative reverse costs in the original curbside graph). The SQL to generate a line graph table is quite simple:
SELECT * into my_linegraph FROM pgr_lineGraph(
'SELECT id, source, target, cost_s as cost, reverse_cost_s as reverse_cost FROM curbs_graph'
);
A snapshot of the resulting line graph is show to the right, more or less depicting the same locations as the earlier figures.
Solver for the street sweeping problem
Once the street data has been cleaned up, the optimal route solver can be set up. The idea for a street sweeper problem is to visit every link. This means every node in the line graph shown above must be visited, and the paths from node to node are given by the links in the graph. Ideally, the street sweeper will sweep every street consecutively, but inevitably there will be a need to “deadhead” over links that have already been swept. The solver’s goal is to minimize the total cost of each vehicle’s path, which means that deadheading will be minimized—any path with avoidable deadheading will be longer than one without. The problem is NP-Hard, so it is unlikely that the optimal solution will be found, but the OR-Tools solver is quite good and can produce quality solutions for 40 routes in about 30 minutes on a recent-vitage laptop.
Many of the details needed for a real-world solution are not available to us yet. For example, most cities prefer to operate their street sweeping and trash hauling routes in zones, in order to facilitate setting parking restrictions and communicating with the public. We also don’t know where the vehicle depot is, where the waste disposal sites are, the operating hours of the vehicles, and so on. The routes we developed without this information are interesting, but ultimately useless in the real world. Without the daily area-restrictions, the generated routes are intertwined like a plate of spaghetti noodles, rather than segmented into discrete areas. Other details like the locations of depots and dump sites mean that the optimization will be off—the dead head trips back to the depot and the dump are not modeled correctly.
Regardless, to illustrate what the solver can do, we generated a GIF of two of the 40 routes, shown to the right (it is a big file so may take a while to download). Each route is a unique color, and in this case you can see red and then blue coverage of links. Even allowing for the fact that we are missing some important information, the routes still look off somehow. If you follow the progress of the sweeper, you’ll see it bop up and down side streets in an area, and then suddenly move on to a different area leaving some side streets untouched. Eventually those streets will get covered, either by the current vehicle or by some other vehicle’s route, but it makes you wonder why skipping those streets is better than hitting them while the vehicle is there already. These skips and jumps might produce a slightly more efficient route, or they might improve the balance of work across vehicles. In practice, however, these skips and jumps will be difficult on the driver. The driver would probably prefer a bit more consistency over a higher global efficiency score.
Thanks for reading all the way to the end. My next post on this topic will get into more details on the solver itself, starting with this initial solver solution, and then what we’ve done within the framework of the OR-Tools vehicle routing solver to improve the generated routes. The full 1 hour “movie” of all 40 routes is a bit mesmerizing, and if you want a copy as a late night sleep aid I’d be happy to post a download link somewhere. Hit me up via the info email link below.